Lacan, lecteur de Peirce et Frege dans le Séminaire XV

*Note aux lecteurs : certains symboles mathématiques utilisés dans ce texte n’étant pas supportés par ce site internet, pour plus de clarté nous invitons les lecteurs à étudier ce texte dans sa version PDF, accessible en cliquant ici

Logique et acte analytique

Peirce et Frege sont aujourd’hui reconnus comme étant les fondateurs de la notion de quantification dans la logique mathématique : leurs frayages marqueront en effet un tournant dans l’histoire de la logique. Lacan y fait expressément référence dans son Séminaire L’Acte analytique, dans la partie que Jacques-Alain Miller a intitulée « explorations logiques ». Pourquoi en effet convoque-t-il ces deux éminents logiciens ? Parce qu’ils ont ouvert, avec quelques autres, la voie à une méthode algébrique visant à symboliser le réel logé dans le langage. Les premiers pas de cette démarche inédite ont très vite abouti à des impasses qui sont à proprement parler celles de la formalisation : « Mais, formule Lacan, c’est le pas originel qui, nous, nous intéresse. Pourquoi ? Parce que nous, analystes, nous nous trouvons en deçà de la tentative de capture de l’énonciation par les réseaux de l’énoncé. Mais quelle chance que le travail ait été poussé si loin ailleurs, si ce peut être là que se livrent à nous quelques règles pour bien repérer la fissure.¹Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, texte établi par J.-A. Miller, Paris, Seuil & le Champ freudien, 2024, p.208. »

Il s’agit en effet pour Lacan d’articuler nouvellement, avec la logique, cette fissure dans l’énoncé corrélative d’un réel de la division du sujet qui ne passe pas dans les réseaux de la symbolisation. C’est à ce niveau qu’il situe le saut de l’acte faisant de l’analysant un analyste. En ce point subtil de fêlure se situe l’évanouissement du sujet supposé savoir comme effet et pivot du transfert ; et c’est précisément là que la notion de quantification dans la logistique entre en jeu. Car il s’agit d’étudier de près le statut logique de l’existence du psychanalyste : « C’est de la logique moderne que nous partirons […], afin de figurer en termes littéraux, en termes d’algèbre logique, en termes de quantification, ce que veut dire Il existe un psychanalyste. C’est grâce à ces figures littérales, en effet, que nous pouvons progresser dans le problème²Ibid., p.179. ». Lacan précise plus loin : « C’est précisément parce que, là, [dans la logique moderne], le sujet supposé savoir n’est rien, et qu’ailleurs, il est fallace, que nous sommes entre les deux, à prendre appui sur la logique d’une part, sur notre expérience de l’autre³Ibid., p.180. ».

Les articulations logiques des pionniers de la logique moderne n’existaient pas avant qu’elles ne surgissent comme telles ; c’est un pas sans précédent dans l’histoire de la logique n’impliquant en effet nul sujet supposé savoir.

C’est pourquoi Lacan scrute les textes fondamentaux de Peirce et de Frege relatifs à la quantification, afin de serrer nouvellement l’acte analytique : « Là où la question se pose de savoir où l’analyste doit se situer […] en acte, nous pouvons trouver secours, du moins ainsi l’ai-je pensé, de la logique⁴Ibid., p.186. ». Il s’agit d’une question, à proprement parler topologique et éthique. Lacan démontre – c’est la thèse que je mets ici à l’épreuve – que dans l’acte analytique, c’est un pas-tous⁵Ibid., p.188. qui permet ce gap où s’institue du psychanalyste, et non le psychanalyste comme prétendue fonction universelle. C’est pourquoi, me semble-t-il, il étudie de près les articulations originelles de la logique mathématique, relatives aux propositions à valeurs universelles et particulières, positives ou négatives.

L’algèbre de Peirce lue par Lacan

Peirce utilise nouvellement des signes algébriques à la place des termes quelques et tout afin de distinguer ceux-ci de façon purement logique, c’est-à-dire littérale : une distinction qui est précisément, selon Peirce, de la même nature que celle entre le vrai et le faux, c’est-à-dire qu’elle est descriptive et non métrique⁶Cf. Peirce C. S., Écrits logiques, Cerf, Paris, 2006, p.283-323. : « la conception métrique serait que toute proposition est plus ou moins fausse, et que la question est une question de degré⁷Ibid., p.283. ».

En suivant le chiffrage de Peirce, considérons ici les propositions respectivement universelle et particulière suivantes⁸Exemples que Peirce choisit lui-même dans l’article que nous considérons ici, datant de 1885. : Tous les rois sont heureux et Quelques rois sont heureux. Peirce pose k pour : Il est roi, et h pour : Il est heureux. Dans la nouvelle algèbre qu’il propose à la communauté scientifique, suivant par là son élève Mitchell,  ?+h signifiera que, de « l’individu » dont on parle, Ou bien il n’est pas roi ou bien il est heureux. Les propositions universelle et particulière s’écriront alors respectivement : Π_i(?_i+h_i) et Σ_i(?_i+h_i). Chacune de ces deux expressions se scinde en une partie booléenne se rapportant à un « individu » (celui dont on parle) et une autre partie quantifiant « les individus » à l’aide d’icônes qui permettent, selon Peirce, de distinguer d’une façon opératoire les termes quelque et tout en les vidant de leurs sens usuels : « Toutes les tentatives, dit-il, pour introduire cette distinction dans l’algèbre booléenne ont été des échecs plus ou moins complets jusqu’à ce que M. Mitchell montre comment cela devait se faire⁹Peirce C. S., Écrits logiques, op. cit., p.297.  ». C’est en effet le problème de l’existence, impliqué par le statut des propositions particulières, qui est au cœur des préoccupations des logiciens de cette époque, problème par ailleurs éludé par le grand logicien George Boole, comme le montre très bien Peirce.

Les symboles iconiques peirciens Σ et Π sont des notations fonctionnelles qui préfigurent respectivement les quanteurs usités aujourd’hui dans la logique mathématique :  et . « Ainsi, dit Peirce, Σi xi signifie que x est vrai de l’un au moins des individus dénotés par i […]. De même, Πi xi signifie que x est vrai de tous ces individus […]. On doit remarquer que Σi xi et Πi xi sont seulement semblables à une somme et un produit ; ils ne sont pas strictement de cette nature, parce que les individus de l’univers peuvent être non-dénombrables¹⁰Ibid., p.299. ».

Il est remarquable – Lacan le souligne – que Peirce soit contraint de passer par une négation du sujet affecté à cet effet d’une barre, quand il écrit les formules comme Σ_i(?_i+y_i) et Π_i(?_i+y_i), pour respectivement les énoncés Quelques x sont y et Tout x est y. La copule logique est ici désignée par le symbole + qui disjoint ? de y ; le signe + a la valeur d’une alternative ambigüe : Ou bien non(x) ou bien y, où y serait impliqué par x ; ce qui s’écrirait, avec le symbole ˅ de la disjonction usité couramment aujourd’hui : ?˅y. L’affirmative universelle proposée par Peirce pourrait alors se dire, en passant par une sorte de double négation, celle du sujet et du prédicat : Pas de roi qui ne soit heureux ou Il n’est de roi qui ne soit heureux.

Un peu avant cette tentative inédite d’algébriser les propositions « quantifiées », Peirce avait établi une figure composée de quatre quadrants¹¹Cf. ibid., p.205. afin de répartir de façon topologique les quatre types de propositions aristotéliciennes ordonnées suivant le carré logique classique des oppositions, figure dont Lacan, on le sait, fera un usage répété dans son enseignement.

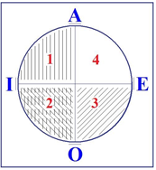
Si, à l’instar de Peirce, on considère trait comme sujet et vertical comme prédicat d’une proposition à articuler, alors l’affirmative positive universelle, notée A dans la logique aristotélicienne, s’énonce : Tous les traits sont verticaux ; la négative universelle E : Tous les traits sont non-verticaux ; la particulière positive I : Il y a quelques traits verticaux ; et la particulière négative O : Il y a des traits non-verticaux.

A est vraie des quadrants 1 et 4 et faux de 2 et 3 ; E est vrai des quadrants 3 et 4 et faux de 1 et 2 ; I est vraie des quadrants 1 et 2 et faux de 3 et 4 ; O est vraie des quadrants 2 et 3 et faux de 1 et 4. On voit par exemple, en lisant les quadrants, que A et E ne se contredisent nullement là où il n’y a nul trait. Si j’affirme que tous les rois sont heureux, s’il n’y en a pas, alors cela ne contredit pas l’affirmation qu’ils sont tous heureux : « les propositions universelles n’impliquent pas, dit Peirce, tandis que les propositions particulières impliquent, l’existence de leurs sujets¹²Ibid., p.205. ». Pour Peirce la fonction de l’universelle est donc corrélative d’un vide où nul trait n’existe, qu’il nomme à l’occasion le Rien.

Lacan propose alors une interprétation saisissante de ces articulations logiques fondamentales et originelles : « ce qui constitue le véritable sujet de toute universelle, dit-il, c’est essentiellement le sujet en tant qu’il est fondamentalement ce Pas de sujet […]. Il est difficile de se maintenir sur ce tranchant. La théorie est très exactement faite pour l’éliminer¹³Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, op. cit., p.205.  ». C’est-à-dire que le sujet de l’énonciation dans un énoncé à valeur universelle fuit et se dérobe, et implique un vide topologique, plus ou moins éludé dans la théorie mathématique de la logique.

Dans ses explorations logiques, Lacan déchiffre très précisément les articulations de Peirce en y faisant saillir la béance entre l’énoncé et l’énonciation, en modulant son dire entre l’écrit et la parole. Si vous dites par exemple, Pas d’homme qui ne soit sage (dans l’algèbre de Peirce : Π_i(?i+s_i), h, pour Il est homme, étant le sujet négativé, et s, pour Il est sage, le prédicat), alors les Non-sages ne sont pas impliqués par le Pas-homme. Mais il peut y avoir après tout de la sagesse qui ne concerne pas l’homme ; non-homme est en effet compatible avec sage : « Or, ceci, formule Lacan, est élidé dans la façon de présenter toute crue la formule de la disjonction, entre un sujet négativé et le prédicat qui ne l’est pas. Il se démontre ainsi que le système dit de la double négation, à s’exprimer de cette scription qui est celle de Mitchell, laisse toujours échapper quelque chose qui, cette fois-ci, loin de suturer la fissure, la laisse à son insu béante. Confirmation que, de fissure, c’est là toujours ce dont il s’agit¹⁴Ibid., p.207.  ».

Qu’est ce qui échappe ? Un réel qui n’entre pas dans la fonction universelle, précisément le réel de la division du sujet : « C’est ce qui nous permet, dit Lacan, d’affirmer que l’opération quantificatrice […], se distingue en ceci de la logique d’Aristote qu’elle substitue – à la place où l’ousia, l’essence, l’ontologique, n’est pas éliminée, à la place du sujet grammatical – le sujet qui nous intéresse en tant que sujet divisé, à savoir la pure et simple division du sujet en tant qu’il parle, du sujet de l’énonciation et du sujet de l’énoncé¹⁵Ibid., p.204-205.  ».

Lacan donne dans cet esprit peircien une transposition clinique en proposant ce mathème : ⒮(?˅S^A), où ⒮ est le sujet divisé, ? le signifiant refoulé et S^A le signifiant fixant le sujet quelque part au lieu de l’Autre¹⁶Cf. ibid., p.217. . Pour tout sujet divisé ⒮, il y a donc ce choix disjonctif homologue à celui des articulations de Peirce : ou bien le signifiant refoulé ? qui le représente auprès de l’autre signifiant S^A, ou bien le signifiant S^A épinglant le sujet dans l’Autre ; S^A laisse non seulement dans l’ombre le signifiant refoulé, mais aussi dans l’oubli le fait même du refoulement. Le premier cas caractérise le versant obsessionnel et la dénégation subséquente, et le second le versant hystérique quant à l’impact du signifiant refoulé traumatique. Nous ne sommes pas ici dans le registre de la mauvaise foi sartrienne, Lacan parlant plutôt de la sincérité et de l’authenticité des sujets en question.

Frege et sa Begriffsschrift¹⁷Cf. Frege G., Idéographie, Vrin, Paris, 1999. Begriffsschrift signifie dans la langue de Frege écriture du concept, traduit par le mot idéographie. Le texte que nous considérons ici a été publié en 1879.

C’est donc au niveau de l’articulation signifiante qu’il faut étudier la fonction des quanteurs et non pas sur le plan de la signification qui est plutôt un effet. Il ne s’agit pas dans cet esprit de quantité d’individus dans la quantification logique, mais de l’usage du signifiant et de la place détectable du sujet de l’énonciation affirmant ou niant un énoncé à valeur universelle ou particulière. Peirce l’a fort bien aperçu. Nulle ontologie n’intervient donc à ce niveau. Frege sur ce point est non seulement radical, mais incontournable, puisque pour lui la logique de la quantification n’est pas relative à un domaine ontologique préétabli. Frege largue en quelque sorte la logique des classes centrée sur la notion d’attribut et d’individu : « je maintiens en effet, nous dit-il, que le concept est antérieur à son extension et considère comme un échec l’effort de tenir l’extension d’un concept pour une classe et celui de la faire reposer non sur un concept mais sur des choses individuelles. Cet effort mène à un calcul de domaine, non à une logique¹⁸Citation prise dans Benmakhlouf A., Gottlob Frege, logicien philosophe, PUF, Paris, 1997, p.85. ».

Lacan considère la logique à l’œuvre dans la Begriffsschrift comme étant « une logique constituante du sujet¹⁹Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, op. cit., p.218. », qu’il nomme sublogique. Tout part en effet chez Frege de sa géniale doctrine du jugement où il congédie l’ontologie : « Dans ma représentation d’un jugement, dit-il, une distinction entre sujet et prédicat n’a pas lieu²⁰Frege G., Idéographie, Vrin, op. cit., p.16. ». Un jugement « est toujours exprimé à l’aide du signe |─── qui se trouve à gauche du signe, ou la combinaison de signes, exprimant le contenu d’un jugement. Si l’on retranche, formule Frege, le petit trait vertical qui se trouve à gauche du trait horizontal, cela a pour effet de transformer le jugement en une simple combinaison d’idées, à propos de laquelle celui qui l’écrit n’exprime pas s’il lui attribue la vérité ou non²¹Ibid., p.15.  ».

Le trait horizontal est ainsi un « trait de contenu » ; le trait vertical, ajouté à gauche du premier trait, est un trait de jugement. Par exemple l’écriture : |───2+3=5 affirme que 2+3 est égal à 5. « On n’a donc pas écrit simplement une valeur de vérité comme dans “2+3=5”, dit Frege, on a dit en même temps que c’est le vrai²²Frege G., Écrits logiques et philosophiques, Seuil, Paris, 1971, p.94. ». Suivant ce fil, Frege écrit l’affirmation de l’implication Si B alors A (équivalente à ?˅A ou à la négation de la conjonction ?ΛB) comme suit :

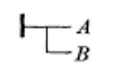
Frege définit alors une fonction « barre horizontale » dont les valeurs sont des valeurs de vérité ; elle s’écrit : ───x ; la valeur de cette fonction est le vrai si le vrai est dénoté par l’argument x, et le faux dans tous les autres cas. Par exemple : « ───2+3=5 » est une proposition vraie, mais « ───1+4=7 » est une proposition fausse.

Avec ces écritures, dont Lacan fait état dans L’Acte analytique, Frege invente ainsi une nouvelle façon d’articuler la relation sujet-prédicat en élargissant le concept de fonction tel qu’il est employé dans la mathématique courante. C’est-à-dire qu’il étend l’écriture fonctionnelle f(x) à des contextes débordants largement celui de l’analyse mathématique. La proposition aristotélicienne A est prédiqué de B joignant un sujet et un prédicat par l’intermédiaire de la copule est, s’écrit alors, dans la logique de Frege, A(B).

Frege vide ainsi les termes de la logique classique des prédicats d’une quelconque référence ontologique : « Le mot “étant” n’est qu’une création du langage pris de court, dit-il, afin de pouvoir rendre applicable la forme du jugement particulier. Quand les philosophes parlent de l’“être absolu”, on a là à proprement parler une divinisation de la copule²³Frege G., Écrits posthumes, Ed. Jacqueline Chambon, Nîmes,1994, p.80. ». Si bien que pour Frege, dans sa Begriffsschrift, « il n’y est pas question de sujet et prédicat dans le sens ordinaire. Notre idéographie, dit-il, est une telle langue [qui n’aurait qu’un seul prédicat pour tous les jugements] et le signe ├─ est son prédicat commun à tous les jugements²⁴Frege G., Idéographie, Vrin, op. cit., p.17. ».

Frege introduit dans cet esprit, corrélativement à la fonction de la barre horizontale : ───x, celle de la négation, c’est-à-dire « celle dont la valeur est le faux quand elle a pour argument les arguments pour lesquels la valeur de ⎯⎯x est le vrai, et dont la valeur est le vrai avec les arguments pour lesquels la valeur de ───x est le faux²⁵Frege G., Écrits logiques et philosophiques, op. cit., p.95. ». Il l’écrit : ─┬─x. Dans ├┬─A, le trait vertical placé sous la barre horizontale du contenu, conjoint avec celui de l’affirmation de fait, situé à gauche du trait du contenu, exprime donc le jugement singulier que le contenu A est faux ou n’a pas lieu comme tel. Une combinaison des différents types de traits, ainsi définis dans la Begriffsschrift, donne des expressions dont la signification se déduit par une lecture : cette signification n’est pas préalable, ça se joue à la lettre. Par exemple les trois jugements²⁶Frege G., Idéographie, Vrin, op. cit., p.24-25. : Si B alors non(A) (équivalent à l’affirmation : A et B s’excluent mutuellement), Si non(B) alors A (équivalent à A ou B), A et B sont réalisés (négation de Si B alors non(A)), s’écriront respectivement dans l’Idéographie de Frege :

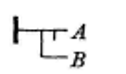
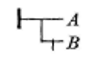
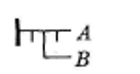
Ces différents types d’implications frégéennes sont analysées et déchiffrées par Lacan afin de montrer ce qu’elles impliquent quant à la nécessité d’une nouvelle articulation de la quantification, promue en effet dans la Begriffsschrift.

La quantification dans la Begriffsschrift de Frege

Pour exprimer un jugement à valeur universelle formulant qu’une fonction Φ dénote toujours le vrai quel que soit son argument, Frege utilise le gramme suivant, un « creux²⁷Frege G., Idéographie, op. cit., p.33. » (dans sa langue : Höhlung) déprimant le trait horizontal :

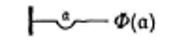
En ajoutant un trait de négation, sous le trait horizontal déprimé, à droite du creux de l’universel, on obtient un jugement universel à valeur négative. Par exemple le jugement Il n’y a aucun X s’écrit²⁸Cf. ibid., p.37. :

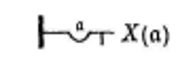
En ajoutant un trait de négation à gauche du creux dénotant l’universel, on obtient un jugement particulier à valeur négative. La proposition Il y a des choses qui n’ont pas la propriété X²⁹Cf. ibid., p.37. s’écrit alors :

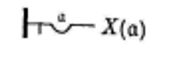
Enfin, avec les deux traits de négation, on obtient un jugement existentiel comme Il existe au moins un Λ³⁰Cf. ibid., p.37.,s’écrivant :

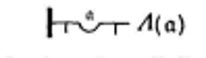
En combinant ces écritures avec le trait de condition on obtient une nouvelle articulation topologique des quatre propositions aristotéliciennes : Tous les X sont des P, Aucun X n’est P, Il existe un X qui est un P, Quelque X ne sont pas des P, s’écrivant en effet respectivement dans la Begriffsschrift³¹Cf. ibid., p.39. :

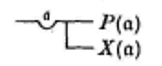
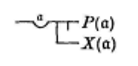
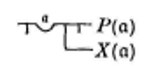
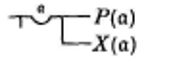
La nécessité de ce creux s’aperçoit selon Frege (Lacan le relève précisément³²Cf. Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, op.cit., p.220.) dans les deux écritures suivantes :

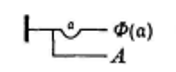
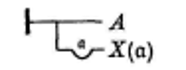
L’une (à gauche) s’articule : Si A alors Tout Φ, l’autre : Si Tout X alors A. Ces deux articulations n’ont pas la même valeur. « Ceci explique, formule Frege, pourquoi le creux avec la lettre gothique écrite à l’intérieur est nécessaire : il délimite le domaine auquel se rapporte la généralité désignée par la lettre. La lettre gothique ne fixe sa signification qu’à l’intérieur de son domaine ; dans un jugement, la même lettre gothique peut apparaître dans différents domaines sans que la signification qu’on lui attribue dans l’un ne s’étende aux autres³³Ibid., p.34. ».

Lacan interprète ⎯ là est le saut ⎯ cette fonction du creux frégéen en montrant que celui-ci est corrélatif de ce qui n’entre pas dans l’écriture du concept : l’objet a.

« L’objet perdu, c’est ce qui vient ici occuper la place qui est donnée dans l’institution de l’universelle affirmative au facteur dit argument dans l’énoncé de Frege, pour quoi la fonction prédicative est toujours recevable. En tout cas, la fonction du tout trouve son assise, son point tournant originel et, si je puis dire, le principe même dont s’institue son illusion, dans le repérage de l’objet perdu, dans la fonction de l’objet a, intermédiaire entre le signifiant originel en tant qu’il est signifiant refoulé, et le signifiant qui le représente dans la substitution qu’instaure la répétition elle-même première.³⁴Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, op .cit., p.223. »

Plus loin Lacan fait référence à la façon dont Frege quantifie la variable dans un jugement à valeur universelle, en lui donnant cette portée clinique essentielle : « L’objet a est singulièrement placé ici pour cette utilisation, qui est logique de sa nature. C’est ce que Frege appellerait, dans l’instauration d’une fonction quelconque F(x), la variable. Si une variable est quantifiée, elle passe à un autre statut. Si elle est précisément quantifiée comme universelle, cela veut dire, non pas simplement n’importe laquelle, mais que foncièrement, dans sa consistance, c’est une constante. Pour l’enfant qui commence d’articuler avec sa demande ce qui fera le statut de son désir, si un objet a la faveur de pouvoir un instant remplir cette fonction constante, c’est le sein.³⁵Ibid., p.225. »

Pour conclure

Au point-cœur de la logique du fantasme, Lacan situe son énoncé Il n’y a pas d’acte sexuel comme corrélative d’une béance du discours³⁶Ibid., p.191. qui ne peut dire, dans un acte signifiant, l’acte sexuel. Ce trou a un étroit rapport, selon lui, avec cette autre béance que Bertrand Russell, lisant justement Frege, avait extraite des écrits de ce dernier : l’univers du discours comme tout n’existe pas.

Lacan montre que la fonction de l’universel dans la logique est en effet « un déplacement de la partie³⁷Ibid., p.240. » : « C’est pour autant que l’objet a, seul, motive et fait surgir la fonction du tout comme telle, que nous nous trouvons en logique soumis à cette catégorie du tout. C’est aussi ce qui explique un certain nombre de singularités qui isolent cette catégorie dans l’ensemble des fonctionnements logiques, ce champ où règne l’appareil quantificateur ⎯ qui l’isolent en y faisant surgir des difficultés singulières, d’étranges paradoxes.³⁸Ibid. »

Par exemple, les manipulations des extensions de concepts comme objets logiques totalisés aboutissent chez Frege à des paradoxes. La réfection des axiomes de la logique, pour écarter ceux-ci, n’empêche pas pour autant le surgissement de nouveaux paradoxes relatifs aux supposées extensions des objets dénotés par une fonction propositionnelle quantifiée. Car la logique, Lacan l’indique à l’occasion, à un certain niveau radical, prend comme objet de son étude l’effet de langage comme tel, pour le systématiser dans un réseau d’énoncés. Mais la faille du sujet de l’énonciation fait obstacle à toute velléité de totalisation. Frege et Peirce nous en apprennent un bout là-dessus, non sans en éprouver un certain malaise. Ils montrent en effet à leur insu que ce qui échappe à leurs machines formelles occupe une place causale dans le développement même de la logique moderne. Car le petit a ne peut être un prédicat logique, pour la simple raison que sur le terme a on ne peut affecter une quelconque négation³⁹Cf. Lacan J., Le Séminaire, livre XV, L’Acte psychanalytique, op. cit., p.227-228.. L’objet a ne qualifie pas à cet égard l’analyste. Cela n’empêche pas l’objet a d’opérer dans le réel, car il s’agit d’un objet – Lacan le montre dans ses leçons – qui a un étroit rapport avec les écritures de la logique moderne.

Dans cet esprit, l’acte analytique c’est le saut du pas-tous.