-
Desargues et le trou de la droite infinie
Le Brouillon project d’une atteinte aux événements des rencontres d’un cône avec un plan de Girard Desargues, publié en 1639, est un texte fondamental quant à l’émergence d’une articulation à proprement parler topologique des fondements mathématiques de la géométrie projective, pressentis par quelques artistes et mathématiciens dont Albrecht Dürer, Johann Werner, Francesco Maurolico et Leon Battista Alberti.
Lacan fera grand cas de ce texte dans son enseignement, notamment dans son séminaire « L’objet de la psychanalyse », lors de ses fameuses leçons consacrées à un commentaire des Ménines de Velázquez. Il y revient à un détour crucial de L’Acte analytique : « Ce qui y domine […], dit-il, c’est une référence que j’ai essayé de vous expliquer dans sa relation avec l’effet de sujet, au moment où la perspective vient dans sa structure propre au niveau de Desargues, c’est-à-dire où elle instaure cette autre définition de l’espace qui s’appelle la géométrie projective1Lacan J., Le Séminaire, Livre xv, L’Acte analytique, texte établi par Jacques-Alain Miller, Seuil & Le Champ freudien, Paris, 2024, p. 246.. » Lacan fonde en effet son analyse des Ménines sur cette intuition géniale de Desargues consistant à adjoindre, à ce qu’il appelle une ordonnance de droites parallèles, un unique point à l’infini commun à celles-ci. Dans le même esprit, pour un faisceau de plans parallèles, il postule une droite à l’infini commune à ces plans, et qu’il nomme un essieu.
Suivant ce fil, il s’avise alors d’une équivalence de la droite infinie avec le cercle, celle-ci se bouclant à l’infini. À partir des principes de la géométrie projective, dont Desargues fraye la voie, on démontre que l’ensemble des directions de l’espace, partant d’un point quelconque de celui-ci, est réductible à un plan dont « l’horizon » est une droite à l’infini de ce même plan, lequel plan est identifiable à l’asphère, soit à la surface d’une sphère où sont identifiés à un même point les points antipodiques : « Le plan projectif autrement dit, de Desargues, formule Lacan, plan dont la découverte comme réduisant son horizon à un point, se précise de ce que ce point soit tel que toute ligne tracée d’y aboutir ne le franchit qu’à passer de la face endroit du plan à sa face envers.2Lacan J., Autres écrits, Seuil, Paris, 2001, p. 471. »
Lacan montre alors la structure projective de l’espace visuel, induite par la pulsion scopique : surface non orientable, à partir de laquelle s’isole et se définit « la fonction de l’objet a qui s’appelle le regard.3Lacan J., L’Acte analytique, op.cit., p. 246. » L’intuition de Desargues, selon laquelle une droite infinie est équivalente à un cercle, est le pivot de son commentaire des Ménines. Ce qui lui sert par ailleurs à bien distinguer la fonction du miroir, où les effets projectifs desarguiens n’existent pas, de celle du tableau : « la perspective organisée, dit-il, c’est l’entrée, dans le champ scopique, du sujet lui-même.4Lacan J., Le Séminaire, Livre XIII, « L’objet de la psychanalyse », leçons du 25 mai 1966, inédite. » Il montre alors comment le regard comme trou vient à déterminer, dans le plan du tableau, une division du sujet entre un point de fuite et le point à l’infini caractéristique de la chute de l’objet regard, situé à la jonction de deux droites parallèles – dans l’essieu constitué par les plans parallèles de la fenêtre et du tableau5Cf. Lacan J., « L’objet de la psychanalyse », op.cit., leçons du 4 et 25 mai 1966, inédites..
Lacan rappelle cette structure fondamentale dans son séminaire « RSI »6Lacan J., Le Séminaire, « R.S.I », Livre XXII, leçons du 8 avril 1975 et 13 mai 1975, texte établi par Jacques-Alain Miller, Ornicar ?, n°5, hivers 1975 /76, p.41 et p.61. Voir aussi la leçon du 11 mars 1975, Ornicar ?, n°5, op.cit, p.21.. Dans l’esprit de ses nœuds il reconsidère en effet l’équivalence desarguienne droite-cercle en proposant des figurations projectives de l’entrelacs borroméen, mettant en jeu deux droites infinies et un cercle (figure 1) ou deux cercles et une droite infinie (figures 2 et 3).
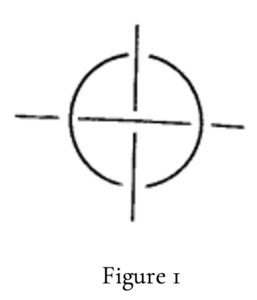
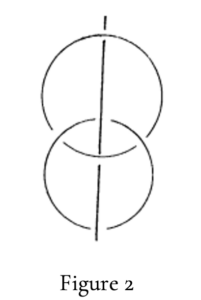

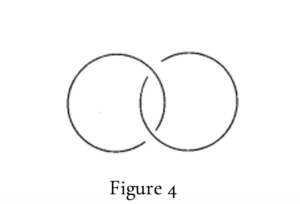
Pour que le nœud tienne, il faut que dans un cas les deux droites infinies ne fassent pas chaîne à l’infini, « d’où qu’on les voie », c’est-à-dire que l’une ne doit pas user du trou de l’autre à la façon de deux anneaux enlacés (figure 4) : « Je vous fais remarquer, formule Lacan en passant, que ce d’où qu’on les voie supporte cette réalité que j’énonce du regard. Le regard n’est définissable que d’un d’où qu’on les voie.7Lacan J., « RSI », 13 mai 1975, Ornicar ?, n°5, op.cit., p.61. Voir aussi Lacan J., Le Séminaire, « R.S.I », Livre XXII, leçon du 10 décembre 1974, texte établi par Jacques-Alain Miller, Ornicar ?, n°2, mars 1975, p.94-95. » Ce regard s’élide en effet dans le plan projectif comme un point à l’infini. Le nœud implique le sujet – coincé comme petit a ; il n’y a pas de sujet du nœud. Si bien que les modalités de bouclage à l’infini nous échappent : la clinique nous les rend sensible.
Desargues ne semble pas s’être préoccupé de la question de savoir comment les droites infinies se nouent effectivement à l’infini ; Lacan s’interroge longuement sur ce point – et tranche le problème en ces termes : « Si nous pensons une droite comme faisant rond d’un point unique à l’infini, comment ne pas voir que ceci a le sens non seulement qu’elles ne se nouent pas, mais que c’est de ne pas se nouer qu’elles se nouent effectivement à l’infini.8Lacan J., «RSI», 13 mai 1975, Ornicar ?, n°5, op.cit., p.61. Voir aussi, Lacan J., Le Séminaire, Livre xxiii, Le sinthome, Seuil, Paris, 2005, p. 114. » Il propose ainsi une nouvelle substance topologique reposant entièrement « sur l’équivalence d’une droite infinie avec un cercle.9Lacan J., Le Séminaire, Livre xxiii, Le sinthome, op.cit., p. 32. » Cette équivalence devient alors le principe même du nœud borroméen.
Il s’agit donc d’un autre mos geometricus « qui résulte de l’efficace propre au langage, et qui se supporte de la fonction du trou10Ibid., p. 32. ». La droite infinie, notée DI dans les notes de Lacan, devient dans cet esprit un nouveau support au trait unaire : « elle est, dit-il, le support le plus simple du trou11Ibid., p. 145. ». Suivant ce fil, il formule que l’inconscient de Freud est « le rapport qu’il y a entre un corps qui nous est étranger et quelque chose qui fait cercle, voire droite infinie, et qui est l’inconscient, ces deux choses étant de toute façon l’une à l’autre équivalentes12Ibid., p. 149. ».
La topologie de la droite infinie permet ainsi de penser autrement la seconde topique de Freud, et ce qu’il a nommé l’Urverdrängt, le refoulé primordial. Nous n’avons qu’à en faire usage.
- 1Lacan J., Le Séminaire, Livre xv, L’Acte analytique, texte établi par Jacques-Alain Miller, Seuil & Le Champ freudien, Paris, 2024, p. 246.
- 2Lacan J., Autres écrits, Seuil, Paris, 2001, p. 471.
- 3Lacan J., L’Acte analytique, op.cit., p. 246.
- 4Lacan J., Le Séminaire, Livre XIII, « L’objet de la psychanalyse », leçons du 25 mai 1966, inédite.
- 5Cf. Lacan J., « L’objet de la psychanalyse », op.cit., leçons du 4 et 25 mai 1966, inédites.
- 6Lacan J., Le Séminaire, « R.S.I », Livre XXII, leçons du 8 avril 1975 et 13 mai 1975, texte établi par Jacques-Alain Miller, Ornicar ?, n°5, hivers 1975 /76, p.41 et p.61. Voir aussi la leçon du 11 mars 1975, Ornicar ?, n°5, op.cit, p.21.
- 7Lacan J., « RSI », 13 mai 1975, Ornicar ?, n°5, op.cit., p.61. Voir aussi Lacan J., Le Séminaire, « R.S.I », Livre XXII, leçon du 10 décembre 1974, texte établi par Jacques-Alain Miller, Ornicar ?, n°2, mars 1975, p.94-95.
- 8Lacan J., «RSI», 13 mai 1975, Ornicar ?, n°5, op.cit., p.61. Voir aussi, Lacan J., Le Séminaire, Livre xxiii, Le sinthome, Seuil, Paris, 2005, p. 114.
- 9Lacan J., Le Séminaire, Livre xxiii, Le sinthome, op.cit., p. 32.
- 10Ibid., p. 32.
- 11Ibid., p. 145.
- 12Ibid., p. 149.


